最高のコレクション (a+b+c)^3 proof 115865-(a+b+c)^3 formula proof

In this video I am going to show you that how you can proof a3b3c3=3abc when abc=0It is a special identity of polynomial of class 9thIt often comes inExample Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3Since B is an empty set, the statement x∈B is false for all x, so (∀x)( x∈Β ⇒ x∈Α ) is also true Thus, B ⊆ Α Since A ⊆ B and B ⊆ Α we have A = B We will use a direct proof here but later we will use another technique to prove this

How Do I Prove 1 A V B C 2 A V C G O G V O Philosophy Stack Exchange

(a+b+c)^3 formula proof

(a+b+c)^3 formula proof-There do not exist prime numbers a, b,and c such that \a^3 b3 = c3\ Although Fermat's Last Theorem implies this proposition is true, we will use a proof by contradiction to prove this proposition For a proof by contradiction, we assume that there exist prime numbers \(a\), \(b\), and \(c\) such that \(a^3 b^3 = c^3\)If the scalar triple product is equal to zero, then the three vectors a, b, and c are coplanar, since the parallelepiped defined by them would be flat and have no volume If any two vectors in the scalar triple product are equal, then its value is zero

A B C 3 Formula Proof

136 ProofsInvolvingSets Example Suppose A andB aresets IfP (A )µP B,then A µB Proof Weusedirectproof AssumeP(A)µP(B) Basedonthisassumption,wemustnowshowthat A µB Toshow AµB,supposethata2 Thentheoneelementset ' a " isasubsetof A,so a " 2P( ) Butthen,sinceP (A )µP B,itfollowsthat aMath a^3 b^3 = (a b)(a^2 b^2 ab) /math Lets try to derive this expansion from the expansion of math (a b) ^ 3 /math We have, math(a b) ^ 3 = a^3Preview Activity \(\PageIndex{2}\) Review of Congruence Modulo \(n\) Let \(a, b \in \mathbb{Z}\) and let \(n \in \mathbb{N}\) On page 92 of Section 31, we defined

The area of whole square is ${(abc)}^2$ geometrically The whole square is split as three squares and six rectangles So, the area of whole square is equal to the sum of the areas of three squares and six rectanglesThe left hand side proof is tricky but here it is, although it would be much easier to use the right hand side given a^3 b^3 c^3 3abc factor a^3 b^3 using cubic formula (ab)(a^2 ab b^2) c^3 3abc now we add 3ab and subtract 3ab at the same time into (a^2 ab b^2) getSince B is an empty set, the statement x∈B is false for all x, so (∀x)( x∈Β ⇒ x∈Α ) is also true Thus, B ⊆ Α Since A ⊆ B and B ⊆ Α we have A = B We will use a direct proof here but later we will use another technique to prove this

Then (A∪B)−C = A∪B = {1,2,3,a} while A∩(B −C)=A∩ B = {3} Can you give different example in which C is nonempty c) (A∪B)−A = B This is also false For a counter example let A and B be as in (a) above Explain why the statement is false d) If A ⊂ C and B ⊂ C, then A∪B ⊂ C This is true and here is why Assume A ⊂ CBut maybe x is in A C not a problem, B∩C is a subset of C, as well, so x not being in C excludes it from being in any subset of C, including the subset B∩C, so in all cases, we see x is in A, but not in B∩C, so x is in A (B∩C), so (A B) U (A C) is a subset of A (B∩C) as well, and the two sets must therefore be equalAs stated in the title, I'm supposed to show that $(abc)^3 = a^3 b^3 c^3 (abc)(abacbc)$ My reasoning $$(a b c)^3 = (a b) c^3 = (a b)^3 3(a b)^2c 3(a b)c^2 c^3 Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers

Prove The A B C 3 A 3 B 3 C 3 3 A B B C C A Brainly In

Example 6 Prove That A 3 B 3 C 3 3abc 1 2 A B C A B

What the rule says is this if have a disjunction in a proof, and you have shown, through a sequence of subproofs, that each of the disjuncts (together with any other premises in the main proof) leads to the same conclusion, then you may derive that conclusion from the disjunction (together with any main premises cited within the subproofs)Math\mathbf B\times\mathbf C/math is a vector purpendicular to the plane formed by math\mathbf B/math and math\mathbf C/math Hence the vector math\mathbf A\times(\mathbf B\times\mathbf C)/math lies in the plane formed by math\mDefinition The longest side of the triangle is called the "hypotenuse", so the formal definition is

Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube

2

What are reasons A, B, and C in the proof?(A and B) A or B De Morgan's law for \and" A )(B )C) (A and B) )C conditional proof In a course that discusses mathematical logic, one uses truth tables to prove the above tautologies 2 Sets A set is a collection of objects, which are called elements or members of the set Two sets are equal when they have the same elements Common Sets(abc)^3 Formula A Plus B Plus C Whole Square (abc)^3 Proof = a^3 b^3 c^3 6abc 3ab (ab) 3ac (ac) 3bc (bc)

2

Nanopdf Com Download Math 431 Homework 4 Due 10 13 Pdf

Then (A∪B)−C = A∪B = {1,2,3,a} while A∩(B −C)=A∩ B = {3} Can you give different example in which C is nonempty c) (A∪B)−A = B This is also false For a counter example let A and B be as in (a) above Explain why the statement is false d) If A ⊂ C and B ⊂ C, then A∪B ⊂ C This is true and here is why Assume A ⊂ CThe area of whole square is ${(abc)}^2$ geometrically The whole square is split as three squares and six rectangles So, the area of whole square is equal to the sum of the areas of three squares and six rectanglesMath\mathbf B\times\mathbf C/math is a vector purpendicular to the plane formed by math\mathbf B/math and math\mathbf C/math Hence the vector math\mathbf A\times(\mathbf B\times\mathbf C)/math lies in the plane formed by math\m

2

If A B C Then B A Cup C Mathematics Stack Exchange

Proof p = a b = 0 @ a 2b 3 a 3b 2 a 3b 1 a 1b 3 a 1b 2 a 2b 1 1 A p0 = a0 b0 = 0 @ ( a 2)( b 3) ( a 3)( b 2) ( a 3)( b 1) ( a 1)( b 3) ( a 1)( b 2) ( a 2)( b 1) 1 A = p The cross product does not have the same properties as an ordinary vector Ordinary vectors are called polar vectors while cross product vector are called axial (pseudo) vectorsOnce you are convinced that a divides b, c − p and c − 2 p and that a = p, replace b by p b ˉ and c − p by p c ˉ Then the equations become (if we divide p out) x 2 b ˉ x c ˉ Condition for exactly one root being common b/w two quadratic equationsOur experiment is a splitsplit plot experiment design (including three independent variables as fixed effects, eg ABC with 3 replicates (1,2,3) and two factors, eg D E as random effects)

Http Facstaff Cbu Edu Wschrein Media M402 notes M402l43 Pdf

What Are Various Forms To Write A B C A Whole Cube Quora

Prove (4 · 3)l (2 · 4)l = l Statements Reasons (4 · 3)l (2 · 4)l = (4 · 3)l (4 · 2)l A _____ = 4(3l 2l) B _____ = 4(5l) Addition = (4 · 5)l C _____ = l Multiplication A Commutative Property of Addition B Distributive Property C Associative Property of Multiplication A Commutative Property of Multiplication B Distributive4 1222 (d) Prove that f(f−1(B)) = B for all B ⊆ Y iff f is surjective Proof =⇒ Let y ∈ Y arbitrary We have to show that there exists x ∈ X with f(x) = y Let B = {y} By assumption, f(f−1(B)) = B = {y}, so y ∈ f(f−1(B))By definition this means that there exists x ∈ f−1(B) with f(x) = yDavneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 9 years He provides courses for Maths and Science at Teachoo

2

Www Math Lsu Edu Adkins M4181 4181f19ps3a

Proof p = a b = 0 @ a 2b 3 a 3b 2 a 3b 1 a 1b 3 a 1b 2 a 2b 1 1 A p0 = a0 b0 = 0 @ ( a 2)( b 3) ( a 3)( b 2) ( a 3)( b 1) ( a 1)( b 3) ( a 1)( b 2) ( a 2)( b 1) 1 A = p The cross product does not have the same properties as an ordinary vector Ordinary vectors are called polar vectors while cross product vector are called axial (pseudo) vectorsWRITE THE PROOF THEOREM Let a, b, and c be integers with a \ne 0 and b \ne 0 If ab and bc, then ac PROOF Suppose a, b, and c are integers where both a and b do not equal to zero Since a divides b, ab, then there exists an integer m such that b = am (Equation #1) Similarly, since b divides c, bc, there exists an integer n such that cThen the 3 points correspond to numbers a, b, c and either a < b < c or c

Http Www Math Lsa Umich Edu Kesmith Cosets Pdf

If A B C Are In Ap Prove That A 3 C 3 6abc 8b 3 Brainly In

"Triangle equality" and collinearity Theorem If A, B, C are distinct points in the plane, then CA = AB BC if and only if the 3 points are collinear and B is between A and C (ie, B is on segment AC) Proof First we prove that the equality is true if B is between A and C Choose a ruler on the line AB;Prove that, abc≥3 Proof The AMGM inequality tells us that, abc √ 3 ≥ abc 3 By substituting abc = 1 and multiplying by 3 we have, abc≥3 Which is what we wanted to prove, so we are doneIn this video I am going to show you that how you can proof a3b3c3=3abc when abc=0It is a special identity of polynomial of class 9thIt often comes in

What Is The Formula For Math A B C 3 Math Quora

Exercises For Chapter 7 1 Prove If Gcd A B C Then Gcd B2 C2

Therefore (6), with a and b interchanged, is identical to (4) Thus since (m 2n 2, 2 ⁢ m ⁢ n, m 2 n 2), as in (4), is a primitive Pythagorean triple, we can say that (a, b, c) is a primitive pythagorean triple if and only if there exists relatively prime, positive integers m and n, m > n, such that a = m 2n 2, b = 2 ⁢ m ⁢ n, andThe abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser It is stated in terms of three positive integers, a, b and c that are relatively prime and satisfy a b = c If d denotes the product of the distinct prime factors of abc, the conjecture essentially states that d is usually not much smaller than c In other words if a and b are composed from large powers of primes, then c is usually not divisible by large powers of primes A number ofProof If n = a 2 b 2, prime q = 3 (mod 4), q n then q a, q b and q 2 nThis reduces to a smaller case n / q 2 = (a / q) 2 (b / q) 2Continued reduction removes primes equal to 3 (mod 4) in pairs, so any sumofsquares solution of n corresponds onetoone to a sumofsquares solution of n / Q = 2 r P if Q is a square, or yields a contradiction implying numsq(n) = 0 if Q is not a

Openresearch Repository Anu Edu Au Bitstream 15 2 B Gupta C K Pdf

If A B C 0 Then How Can You Prove A 3 B 3 C 3 3abc Quora

A and b are the other two sides ;So x IS in AC and x is NOT in BC, so x IS in (AC)(BC) that's "half" of the proof the "other half" starts with assuming x is in (AC)(BC) Log in or register to reply now!Sample Proof a(BC)=aBaC Given mxn matrices B and C, and scalar a, prove a(BC)=aBaC Proof To show that the matrices a(BC) and aBaC are equal, we must show they are the same size and that corresponding entries are equal Same size Since B and C are mxn, BC is mxn thus a(BC) is mxn also Since B is mxn, aB is mxn

Www Cs Uaf Edu Faudree M401h7s Pdf

A3

It is called "Pythagoras' Theorem" and can be written in one short equation a 2 b 2 = c 2 Note c is the longest side of the triangle;(1) Let A, B, and C be sets such that (A\C) (B \C) and (AC) (B C) f* State your contradictory suppositiong (2) By way of contradiction, suppose A * B f* Pick a suitable element to start your element argumentg (3) Since A * B, there exists x 2A such that x =2y negating de nition of subset f* Use logic, together with hypotheses, to traceProve (4 · 3)l (2 · 4)l = l Statements Reasons (4 · 3)l (2 · 4)l = (4 · 3)l (4 · 2)l A _____ = 4(3l 2l) B _____ = 4(5l) Addition = (4 · 5)l C _____ = l Multiplication A Commutative Property of Addition B Distributive Property C Associative Property of Multiplication A Commutative Property of Multiplication B Distributive

Inequalities From The Word 1995 05

2

Asked Jan 30, 18 in Class IX Maths by ashu Premium (930 points) Prove that (a b c) 3 a 3 b 3 – c 3 =3 (a b) (b c) (c a) polynomialsThe following proof is very similar to one given by Raifaizen By the Pythagorean theorem we have b 2 = h 2 d 2 and a 2 = h 2 (c − d) 2 according to the figure at the right Subtracting these yields a 2 − b 2 = c 2 − 2cd This equation allows us to express d in terms of the sides of the triangleOnce you are convinced that a divides b, c − p and c − 2 p and that a = p, replace b by p b ˉ and c − p by p c ˉ Then the equations become (if we divide p out) x 2 b ˉ x c ˉ Condition for exactly one root being common b/w two quadratic equations

Prove A B C 3 A 3 B 3 C 3 3 A B B C C A Mathematics Topperlearning Com 9j3ovqff

Vector Analysis By Alimkanwalimtinaa Issuu

Math a^3 b^3 = (a b)(a^2 b^2 ab) /math Lets try to derive this expansion from the expansion of math (a b) ^ 3 /math We have, math(a b) ^ 3 = a^3Chapter 2 1 Prove or disprove A − (B ∩ C) = (A − B) ∪ (A − C) Ans True, since A−∩()BC=A∩B∩C=A∩()B∪C=(A∩BA)∪()∩C=(A−BA)∪−(C) 2 Prove that AB∩=A∪B by giving a containment proof (that is, prove that the left side is a subset of the right side and that the right side is a subset of the left side)Mentally examine the expansion of math(xyz)^3/math and realize that each term of the expansion must be of degree three and that because mathxyz/math is cyclic all possible such terms must appear Those types of terms can be represented

Http Btravers Weebly Com Uploads 6 7 2 9 Problem Set 3 Solutions Pdf

A B C 3 Formula Proof

Prove using conditional proof 1 1 A B C 2 B E 3 C E X A X Answer 4 A ACP 5 B C from ENG 6301 at Mapúa Institute of TechnologyAn Alternative Sine Rule Proof a/sinA = b/sinB = c/sinCVideo by Tiago Hands (https//wwwinstagramcom/tiago_hands/)Instagram ResourcesMathematics ProofsForums Homework Help Calculus and Beyond Homework Help Hot Threads From solution to mother equation

Prove That A B C 3 A3 C3 3 A B B C C A Math Polynomials Meritnation Com

Methods Of Proof Lecture 4 Sep 16 Chapter 3 Of The Book Ppt Download

Transcript Misc 5 Introduction Show that if A ⊂ B, then C – B ⊂ C – A Let A = {1, 2} , B = {1, 2, 3}, C = {1, 2, 3, 4} C – B = {1, 2, 3, 4} – {1, 2, 3What are reasons A, B, and C in the proof?If I have the elements from sets A and B, and I want to find the set A ∪ (B ∩ C), I end up with just the elements of A On the other hand, if I have the elements from A and B and want to find (A ∪

What Are Various Forms To Write A B C A Whole Cube Quora

2

C 2 = (b a) 2 − 2 a b = a 2 b 2 c^{2}=(ba)^{2}2ab=a^{2}b^{2} c 2 = (b a) 2 − 2 a b = a 2 b 2 A related proof was published by future US President James A Garfield Instead of a square, it uses a trapezoid, which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner

Http Users Math Msu Edu Users Robertbe Mth310sp11homework S3 Pdf

Http Pi Math Cornell Edu Ebs Math3040 Hw3 Pdf

Www Math Fsu Edu Hoeij Spring19 Mgf3301 Sampletests Test2fall15answers Pdf

2 5 Proving Statements About Segments Ppt Video Online Download

Proof Of 501 C 3 Warrior Outdoors

Prove Consequences Of The Field Axioms Stumbling Robot

Pdf A New Proof Of Watson S Theorem For The Series 3f2 1

22 Prove If A B And C Are Odd And A B C And A Then A B And A C 22 Prove If A B And C

Web Maths Unsw Edu Au Mikeh Webpapers Paper98 Pdf

Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube

2 When Is A 2 Digit Number The Sum Of The Squares Of Its Digits Pdf Free Download

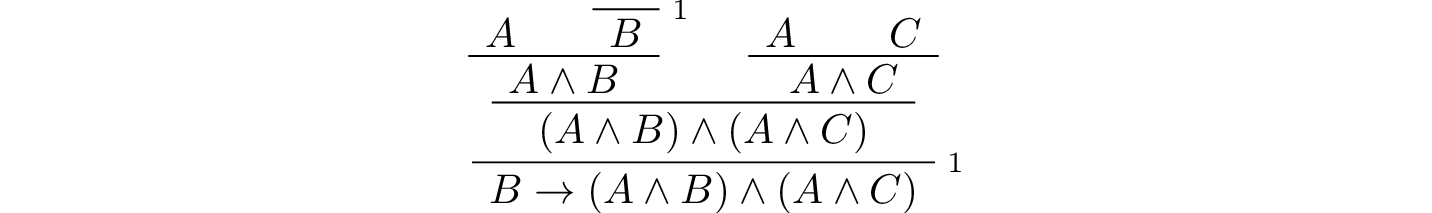
3 Natural Deduction For Propositional Logic Logic And Proof 3 18 4 Documentation

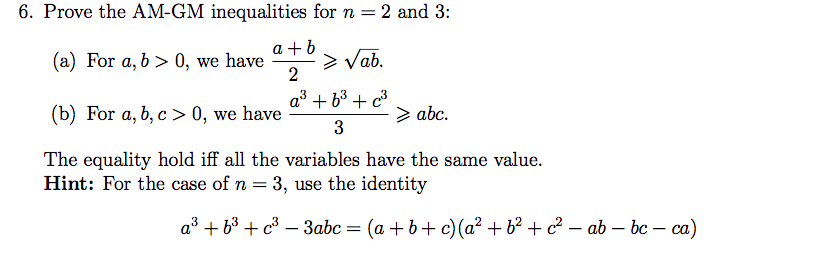
Solved 6 Prove The Am Gm Inequalities For N 2 And 3 T Chegg Com

Http Www Thebookshelf Auckland Ac Nz Docs Maths Pdf Mathschron004 003 Pdf

2

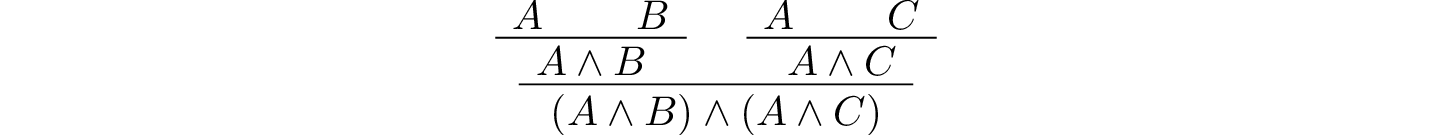
3 Natural Deduction For Propositional Logic Logic And Proof 3 18 4 Documentation

Answered 76 Chapter 2 Sets And Whole Numbers 11 Bartleby

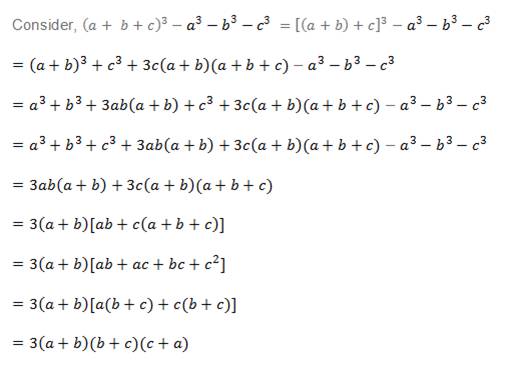
Prove That A B C 3 A3 C3 3 A B B C C A Polynomials Maths Class 9

What Is The Expansion Of A B C 3 Quora

Two Column Proofs Given 2x 3 2 3 Prove X 11 6 Statements Ppt Download

Ppt Chapter 3 Homework Review Exercises 2 7 2 3 6 7 Are Correct Powerpoint Presentation Id

Http Oregonstate Edu Instruct Mth341 Garity Fall00 Section1 4 Pdf

Q Tbn And9gcsectilf2waloldhrvvptyk0gppw0kxl9fe R8 Qft5iyl5p4g2 Usqp Cau

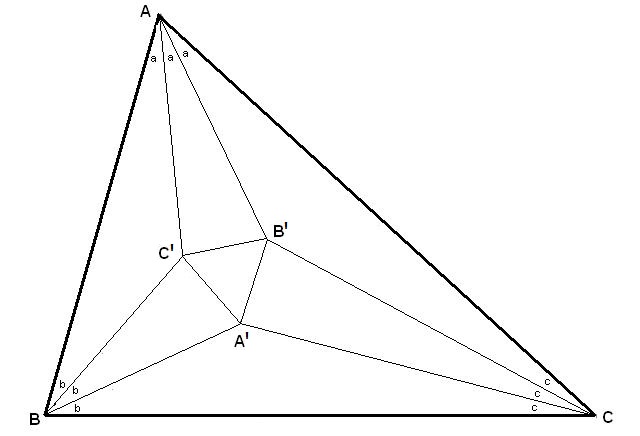
Math Garden Morley S Theorem

Solved Here Is A Proof That 3 4 Let A B And C Be Any T Chegg Com

Solved Let A B And C Be Sets Present A Direct Proof For Chegg Com

Answered Let Bo B Bz Be The Sequence Bartleby

How Do I Prove 1 A V B C 2 A V C G O G V O Philosophy Stack Exchange

2

Faculty Math Illinois Edu Rtramel Math418spring17hw4 Pdf

Http Faculty Missouri Edu Cutkoskys Modalghand1 Pdf

Http Math Bu Edu People Rpollack Teach 129fall10 129midterm1 Solns Pdf

2

2

A B C 3 Formula Proof

Solved 12 Evaluation Of Proofs See The Instructions For Chegg Com

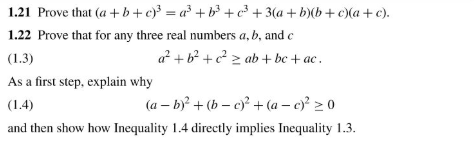
Solved 1 21 Prove That A B C 3 A3 C3 3 A B Chegg Com

Www Math Tamu Edu Boggess Math222 Hwsolutions Sampleproof Pdf

Prove That There Do Not Exist Prime Numbers A B And C Such That A 3 B 3 C 3 Prove It By Using The 4 Cases Use A Correct And Complete English Sentence

Search Q A B C 5e3 Tbm Isch

A 3 B 3 C 3 3abc Formula A B 2 A 2 B 2 2ab Proof Derivation Of Algebraic Identities Youtube Youtube

2

Proof Of Pappus S Theorem If A B C Are 3 Collinear Points As Well Download Scientific Diagram

2

Inequalities Marathon

A 3 B 3 C 3 3abc Formula Proof

2

Cseweb Ucsd Edu Classes Sp09 Cse140 Mid1samp Sol Pdf

Www Cs Csustan Edu Mmartin Teaching Math2300s16 Homework 2300 Ch5 Homework Pdf

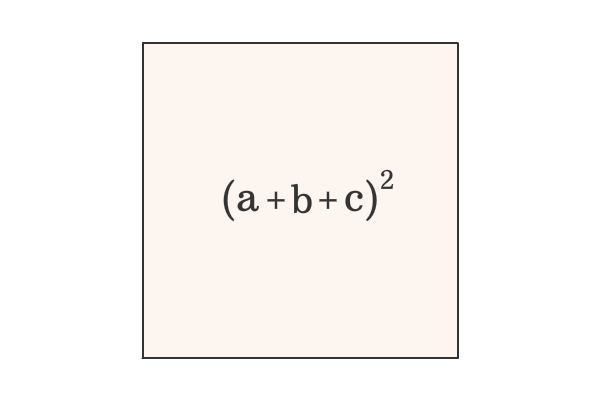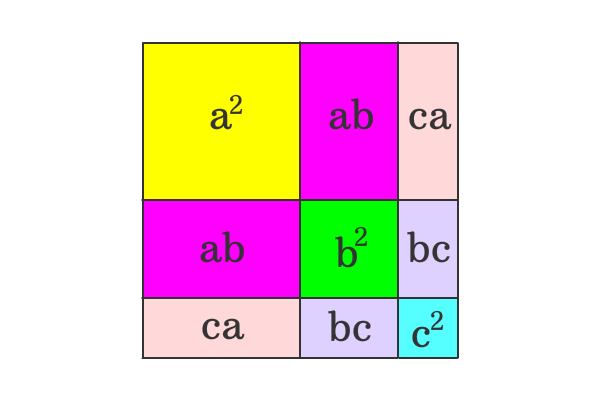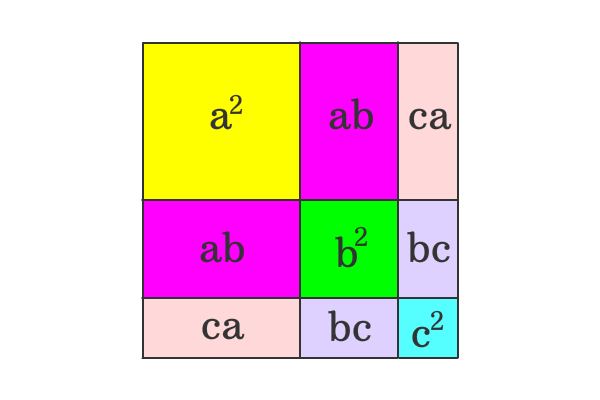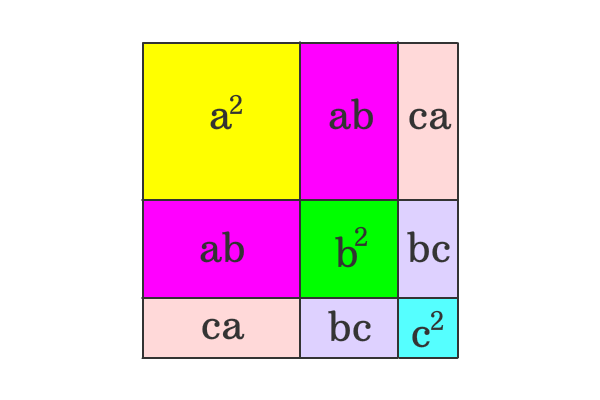
Proof Of A B C Formula In Geometric Method

Search Q A 5e3 2bb 5e3 2bc 5e3 Formula Tbm Isch

Http Granite Sru Edu Lmiller Course Materials 3 Zhw 3 Sol05 S08 Pdf

2

Prove That Tex A B C 3 A 3 B 3 C 3 3 A B B C C A Tex Brainly In

Solved Annotate All Your Proofs With Comments Text In Ord Chegg Com

Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube

Condor Depaul Edu Ntomuro Courses 400 Notes Lecture4 Pdf

Natural Deduction Proof For A To B To C To A To B To A To C Mathematics Stack Exchange

2

Inequalities Marathon

Search Q A 5e3 2bb 5e3 2bc 5e3 3abc Tbm Isch

What Is The First Line Of The Proof 1 If A Divides B Then A Divides B C 2 If A Divides B Then A Divides C 3 Assume A Divides

Users Math Msu Edu Users Siefring Mth421 S10 Hw Hw5sol Pdf

2

Prove That A3 C3 3abc 1 2 A B C A B 2 B C 2 C A 2 Brainly In

Users Math Msu Edu Users Mrathbun Teaching 108ssi10 108ssi10 Homeworksolns Hw2sol Pdf

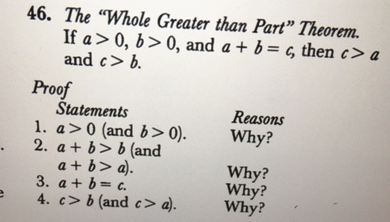
The Whole Greater Than Part Theorem If Math A Gt0 Math Math B Gt0 Math And A B C Then Math C Gt A Math And Math C Gt B Math Proof Math Begin Array Ll Text Statements Text Reasons 1 A Gt0 Text And B Gt0 Text Why

The Inequality Frac A 4 A 3 B 3 Frac B 4 B 3 C 3 Frac C 4 C 3 A 3 Ge Frac A B C 2 Mathematics Stack Exchange

2

Proof That Metric Spaces Are Paracompact

2

2

Toddgutekunst Files Wordpress Com 15 08 Proofs 2 3 Pdf

Http Www Thebookshelf Auckland Ac Nz Docs Maths Pdf Mathschron004 003 Pdf

Incoming Term: (a+b+c)^3 proof, (a+b+c)^3 formula proof, a^3+b^3+c^3-3abc proof, a^3+b^3+c^3-3abc formula proof,